Αστρολάβος........Φυσικής: 2.5 Ανάκλαση- Διάθλαση

Εμφάνιση αναρτήσεων με ετικέτα 2.5 Ανάκλαση- Διάθλαση. Εμφάνιση όλων των αναρτήσεων

Τετάρτη 16 Σεπτεμβρίου 2009

Ανάκλαση - Διάθλαση (video)

Όταν το φως που διαδίδεται σ' ένα μέσο συναντήσει τη διαχωριστική επιφάνεια ανάμεσα σ' αυτό το μέσο διάδοσης και σ' ένα άλλο, τότε ένα μέρος του αλλάζει διεύθυνση και επιστρέφει στο αρχικό μέσο διάδοσης. Το φαινόμενο αυτό ονομάζεται ανάκλαση και διακρίνεται σε

Κατοπτρική ανάκλαση,

Διάχυση.

Η κανονική ( ή κατοπτρική ) ανάκλαση έχουμε όταν παράλληλες ακτίνες προσπίπτουν σε λεία επιφάνεια και ανακλώνται επίσης παράλληλα. Όταν οι ακτίνες μιας φωτεινής παράλληλης δέσμης πέσουν πάνω σε μια λεία και στιλπνή επιφάνεια (κάτοπτρο), ανακλώνται. Οι ανακλώμενες ακτίνες εξακολουθούν να είναι παράλληλες μεταξύ τους, όπως φαίνεται στο σχήμα. Η ανάκλαση αυτή ονομάζεται κατοπτρική ανάκλαση.

Η διάχυση έχουμε όταν παράλληλες ακτίνες προσπίπτουν σε τραχιά επιφάνεια και ανακλώνται προς τυχαίες κατευθύνσεις. Στην περίπτωση όπου οι ακτίνες της φωτεινής παράλληλης δέσμης πέσουν πάνω σε μια επιφάνεια η οποία έχει ανωμαλίες, οι ακτίνες που την αποτελούν ανακλώνται σε διάφορες κατευθύνσεις. Έτσι οι ανακλώμενες ακτίνες δεν είναι πια παράλληλες μεταξύ τους. Η ανάκλαση αυτή ονομάζεται διάχυση.

Νόμοι της ανάκλασης

α) Η προσπίπτουσα ακτίνα, η ανακλώμενη ακτίνα και η κάθετος στην επιφάνεια στο σημείο πρόσπτωσης βρίσκονται πάντα στο ίδιο επίπεδο.

β) Η γωνία ανάκλασης (θ_α) είναι ίση με τη γωνία πρόσπτωσης (θ_π), δηλαδή: θ_π= θ_α

Δείτε το παρακάτω σχήμα:

Ανάκλαση από επίπεδο κάτοπτρο:
Η γωνία πρόσπτωσης είναι ίση με την γωνία ανάκλασης (θ = θ΄)

Τώρα παρακολουθήστε το παρακάτω video

Διάθλαση :
Θεωρούμε δύο οπτικά μέσα στα οποία το φως διαδίδεται με διαφορετική ταχύτητα. Αν το φως περάσει από το ένα μέσο στο άλλο, ένα μέρος του ανακλάται και το υπόλοιπο διαθλάται, δηλαδή διαδίδεται στο δεύτερο μέσο με διαφορετική διεύθυνση από την αρχική. Το φαινόμενο αυτό ονομάζεται διάθλαση. Η γωνία που σχηματίζει η διαθλώμενη ακτίνα με την κάθετο στη διαχωριστική επιφάνεια των δύο μέσων ονομάζεται γωνία διάθλασης (θ_δ).
Η σχέση που συνδέει τη γωνία πρόσπτωσης με τη γωνία διάθλασης, ως προς την κάθετο, στη διαχωριστική επιφάνεια είναι γνωστή ως "νόμος του Snell".

$n_1sin\theta_1=n_2sin\theta_2 \,$

Ορισμοί

Γωνία πρόσπτωσης χαρακτηρίζεται η σχηματιζόμενη γωνία από την διεύθυνση της ακτίνας με την κάθετο του σημείου πρόσπτωσής της.
Γωνία διάθλασης χαρακτηρίζεται η σχηματιζόμενη γωνία από την διαθλώμενη ακτίνα με την ίδια κάθετο του σημείου εισόδου στο διαπερατό μέσο. Όταν ακτίνες φωτός κινούνται από αραιότερο μέσον σε πυκνότερο η γωνία διάθλασης είναι πάντα μικρότερη της προσπίπτουσας. Το αντίθετο συμβαίνει από πυκνότερο σε αραιότερο μέσο.
Επίπεδο διάθλασης χαρακτηρίζεται το επίπεδο που ορίζεται από τη προσπίπτουσα και ανακλώμενη ακτίνα.
Κανονική διάθλαση ονομάζεται η εκτροπή μιας ακτίνας όταν περνάει από ένα μέσο σε άλλο που χωρίζονται μεταξύ τους από μια λεία επιφάνεια.
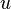Δείκτης διάθλασης (index of refraction) χαρακτηρίζεται το μέτρο της εκτροπής (ή κάμψης) που υφίσταται μια ακτίνα διερχόμενη από ένα διαπερατό μέσον σε άλλο. Ορίζεται ως ο λόγος της ταχύτητας διάδοσης του φωτός "κενό" $c \,$ προς την ταχύτητα διάδοσης στο υπό εξέταση διαπερατό μεσο $u \,$ . Iσχύει δηλαδή

$n=\frac{c}{u}$

Από τον παραπάνω ορισμό φαίνεται πως ο δείκτης διάθλασης του κενού ισούται με τη μονάδα. Έτσι, στην περίπτωση όπου έχουμε μετάδοση ακτινοβλίας από το κενό σε ένα οπτικό μέσο με δείκτη διάθλασης $n \,$ , ο τελευταίος μπορεί να οριστεί συναρτήσει των γωνιών πρόσπτωσης και διάθλασης, $\theta_1 \,$ και $\theta_2 \,$ αντίστοιχα:

$n=\frac{\sin \theta_1}{\sin \theta_2}$

Κάθε διαπερατό σώμα (μέσον) έχει ιδιαίτερο δείκτη διάθλασης, που εξαρτάται από τα φυσικά χαρακτηριστικά του. Στην ιδιότητα αυτή στηρίζονται πολλοί έλεγχοι τροφίμων π.χ. του βουτύρου, καθώς το αγνό βούτυρο έχει άλλο δείκτη από εκείνο του νοθευμένου, όπως συμβαίνει και με διάφορα λάδια κ.α. υγρά.

Δείτε την εικόνα:

n1. Η ταχύτητα είναι μικρότερη στο δεύτερο μέσο (u2 <>

Διάθλαση του φωτός στην επιφάνεια μεταξύ δύο μέσων διαφορετικών δεικτών διάθλασης, με

n 2 > n 1

. Η ταχύτητα είναι μικρότερη στο δεύτερο μέσο (

u 2 < u 1

), οπότε και η γωνία διάθλασης

θ 2

είναι μικρότερη από τη γωνία πρόσπτωσης

θ 1

Σημείωση στο διάγραμμα η διακεκομμένη ευθεία, είναι η κάθετος, στην επιφάνεια πρόσπτωσης.

Δείτε ένα video:

Στο προηγούμενο video προσπαθεί και βρίσκει την ορική ή κρίσιμη γωνία.

Κρίσιμη γωνία ή οριακή

Όταν το φως διέρχεται από ένα πυκνότερο σε ένα αραιότερο μέσο τότε η γωνία πρόσπτωσης μπορεί να παίξει σημαντικό ρόλο. Όταν η γωνία πρόσπτωσης ξεπεράσει μια κρίσιμη τιμή (η οποία εξαρτάται από τα μέσα από τα οποία διέρχεται το φως) τότε δεν υπάρχει εξερχόμενη από το μέσο ακτίνα φωτός. Το φαινόμενο αυτό ονομάζεται ολική ανάκλαση του φωτός. Στην εικόνα που ακολουθεί μπορούμε να παρατηρήσουμε αυτό ακριβώς το φαινόμενο. Ακτίνες φωτός ξεκινάνε μέσα από το νερό και κατευθύνονται προς τον αέρα. Όταν οι ακτίνες φωτός έχουν γωνία πρόσπτωσης που δεν ξεπερνάει αυτήν την κρίσιμη τιμή, τότε βλέπουμε και την εξερχόμενη ακτίνα. Όταν όμως φτάσουμε ή ξεπεράσουμε αυτήν την τιμή, δεν υπάρχει εξερχόμενη ακτίνα.

Κρίσιμη ή οριακή γωνία ονομάζουμε την τιμή της γωνίας πρόσπτωσης για την οποία η διαθλώμενη κινείται παράλληλα στη διαχωριστική επιφάνεια

ΣΥΜΠΕΡΑΣΜΑ

Όταν η φωτεινή ακτίνα μεταβαίνει από οπτικά πυκνότερο σώμα σε αραιότερο, αλλά η γωνία προσπτώσεως είναι μεγαλύτερη μιας τιμής, εξαρτώμενης από τη φύση των δύο μέσων (ορική γωνία), τότε ανακλάται ολικώς.

Πηγές:
1. http://www.clab.edc.uoc.gr/seminar/heraklio/optic/index.htm
2. Παναγιωτακόπουλος,Γ. ,Μαθιουδάκης Γ., (2009),Φυσική Γ΄Λυκείου,Εκδ. Σαββάλας
3. wikipedia
4. http://en.wikipedia.org/wiki/Refraction

Τετάρτη 15 Οκτωβρίου 2008

Διάθλαση και αρχή ελαχίστου χρόνου

Με αφορμή μια ερώτηση στην τάξη γράφω δυο λόγια για τη διάθλαση, την αρχή του ελαχίστου χρόνου και τον νόμο του Snell.

Όταν το φως διασχίζει την επιφάνεια που χωρίζει δυο μέσα (διαχωριστική επιφάνεια) και περνά από το ένα μέσο στο άλλο, λέμε ότι διαθλάται γιατί αλλάζει η διεύθυνση διάδοσης του (εκτός αν πέφτει κάθετα) και το φαινόμενο το ονομάζουμε διάθλαση. Συνήθως όταν το φως αλληλεπιδρά με την ύλη εν μέρει απορροφάται , εν μέρει ανακλάται και διαθλάται.

Είναι κοινή παρατήρηση και φαίνεται και στην εικόνα ότι η διαδρομή επιμηκύνεται. Ωστόσο η μακρύτερη αυτή διαδρομή είναι αυτή που απαιτεί τον ελάχιστο χρόνο.

Σύμφωνα με την αρχή του ελαχίστου χρόνου, που είναι γνωστή και σαν αρχή του Φερμά (Fermat principle), το φως κατά τη διαδρομή του μέσα σε ένα μέσο από ένα σημείο Α σε ένα σημείο Β, ακολουθεί τον οπτικό δρόμο που θα του επιτρέψει να μεταβεί από το Α στο Β στο μικρότερο δυνατό χρόνο. Η αρχή αυτή διατυπώθηκε για πρώτη φορά από τον μαθηματικό (Pierre de Fermat) την Πρωτοχρονιά του1662.
Σε ένα ισότροπο μέσο (n=Σταθερό) ο οπτικός αυτός δρόμος είναι η ευθεία που ενώνει τα σημεία Α και Β. Όταν όμως το κύμα περάσει από ένα μέσο σε άλλο με διαφορετικό δείκτη διάθλασης, ο χρονικά συντομότερος δρόμος δεν είναι ευθεία, επειδή η ταχύτητα του κύματος είναι διαφορετική στα δυο μέσα. Ο χρονικά συντομότερος δρόμος τότε είναι μια τεθλασμένη γραμμή, με αποτέλεσμα να παρουσιάζεται το φαινόμενο της διάθλασης.

Ας το κάνουμε λίγο πιο απλό. Έστω ότι είστε ναυαγοσώστης σε μια παραλία και αντιλαμβάνεστε ότι κάποιος κινδυνεύει.Οι ενέργειες σας για τη διάσωση του κολυμβητή πρέπει να είναι άμεσες. Ποια διαδρομή από το Π στο Θ πρέπει να ακολουθήσετε για να φτάσετε στον κολυμβητή το συντομότερο δυνατόν; (Υπόδειξη: Θεωρήστε ότι μπορείτε να αναπτύξετε ταχύτητα στην παραλία μεγαλύτερη απ' ό,τι στη θάλασσα.)

Αν η κίνηση σας ήταν ευθύγραμμη δεν θα ήταν αυτή που θα διαρκούσε το λιγότερο χρόνο διότι θα διανύατε μεγαλύτερη απόσταση στη θάλασσα που κινείστε με μικρότερη ταχύτητα. Αν ξοδεύατε λίγο περισσότερο χρόνο τρέχοντας μεγαλύτερη απόσταση στη στεριά θα κερδίζατε πολύ περισσότερο χρόνο για τη μικρότερη διαδρομή στη θάλασσα. Άρα η σωστή διαδρομή θα ήταν η ΠγΘ.

Για να βρούμε την πορεία του φωτός από το ένα μέσο στο άλλο χρησιμοποιούμε το νόμο του Snell. Βέβαια το νόμο στην ουσία τον είχε ανακαλύψει ένας Άραβας - Ali ibn Sahl Rabban al-Tabari- (μαθηματικός, φυσικός και μηχανικός φακών ) που το 984 περίπου έγραψε το On Burning Mirrors and Lenses που εξηγούσε πως οι κυρτοί και κοίλοι καθρέπτες και φακοί εστίαζουν και κυρτώνουν την πορεία του φωτός.
Μελετά με λεπτομέρειες την ανάκλαση και τη διάθλαση και διατυπώνει την υπόθεση, ότι το φως διαδίδεται πιο δύσκολα στα οπτικά πυκνότερα υλικά, και στο γεγονός αυτό οφείλεται η διάθλασή του.
Διατυπώνει την άποψη ότι οι φωτεινές ακτίνες κινούνται σε ευθεία γραμμή.
«Δεν υπάρχει όραση», γράφει στην οπτική του, «εκτός και αν κάτι εκκινεί από το ορατό αντικείμενο και φτάνει στο μάτι, ανεξάρτητα από το αν κάτι εξέρχεται από αυτό.

Το 1621 ο Δανός Φυσικός -Μαθηματικός Willebrord Snellius ή αλλιώς Willebrord Snellius διατύπωσε το νόμο της διάθλασης.

Ένα ωραίο site με φωτογραφίες και πειράματα είναι το παρακάτω:

http://www.clab.edc.uoc.gr/seminar/heraklio/optic/index.htm

Και επειδή μας έγινε συνήθεια, ας δούμε και μερικά video με οπτικά φαινόμενα.

2. Δείτε το παρακάτω video στο youtube. Περιγράφει την ανάκλαση και τη διάθλαση με πειράματα. Πραγματικά αξίζει! http://www.youtube.com/watch?v=2P3nKJHO2j0
Πηγές:
1. http://en.wikipedia.org/wiki/Main_Page
2. Hewitt,P (2005) Οι έννοιες της Φυσικής, ΠΕΚ, Ηράκλειο
3. Epstein,L (2002)Στις γειτονιές της Φυσικής, Κάτοπτρο,Αθήνα.
4. http://gkatsikogiorgos.blogspot.com/2008/08/blog-post.html